Data Visualization with Big Data
Why visualize?
- We’ve already seen that visualizations are an important data analysis tool (Loftus)
- Visualization for analysis vs. visualization for communication:
- “Reveal relationships in large datasets…”
- “…and communicate information to a broad audience”
- Not necessarily the same thing!
Reveal relationships
… in large datasets?
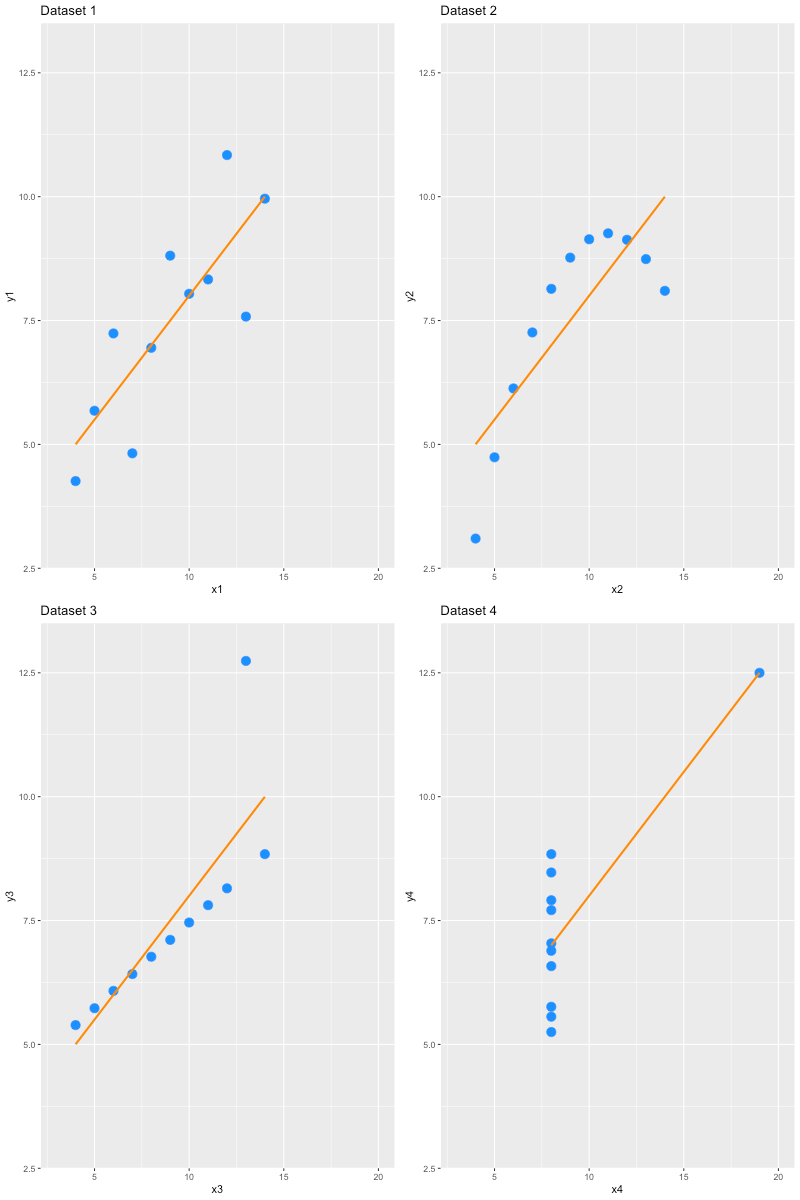
A few basic items
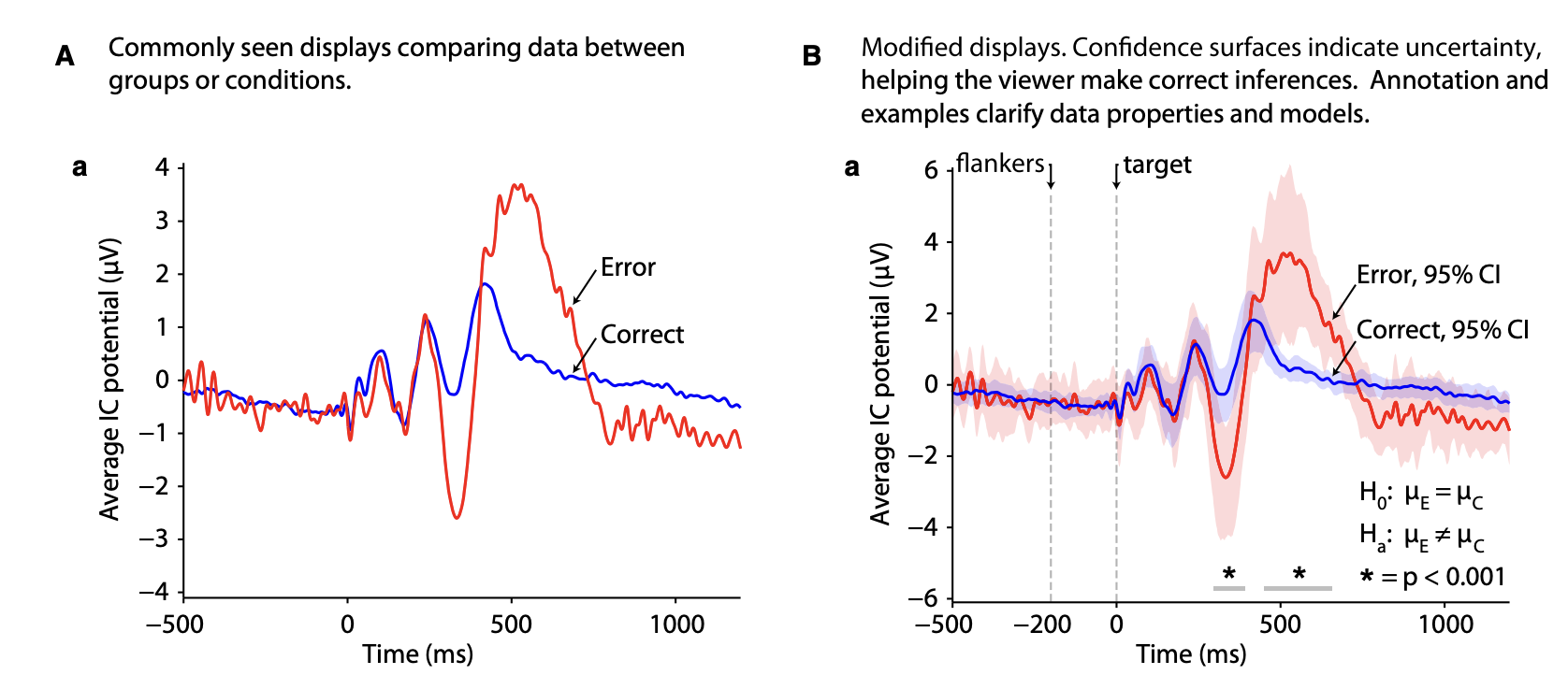
From Allen et al. (2012)
- Are the axes labeled?
- Are scales and units indicated?
- Is there a measure of uncertainty (e.g., error bars)?
- Is the type of uncertainty (e.g., SEM, CI, …) indicated?
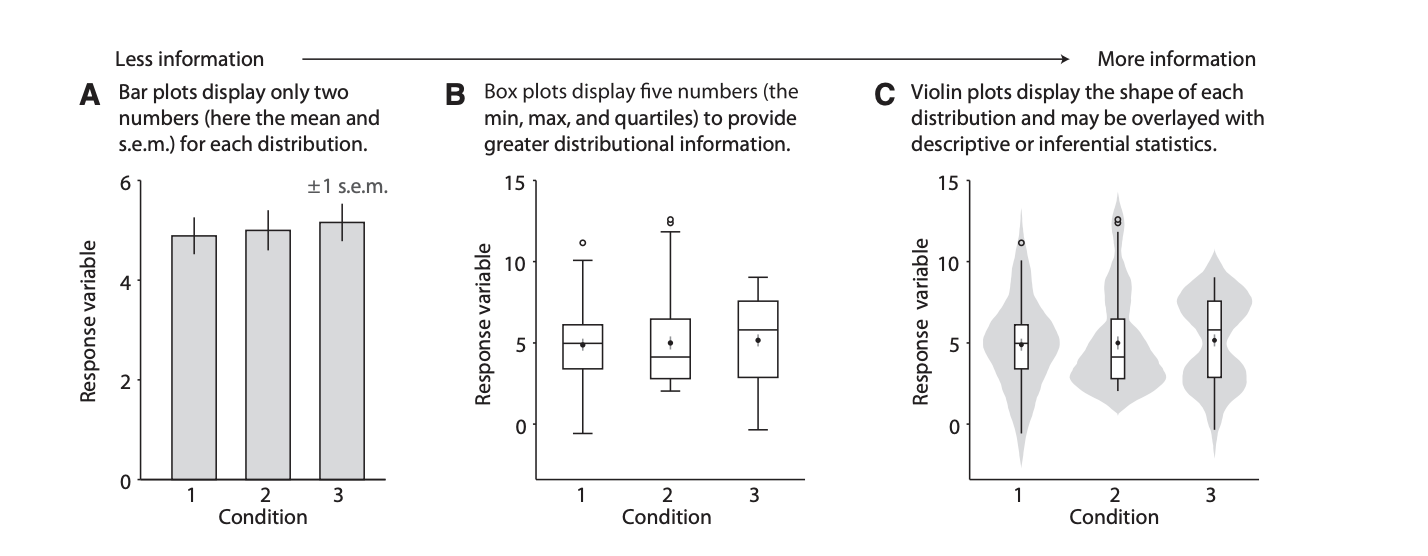
Show more, hide less
- From bar plots …
- … to box plots …
- … to swarm plots, violin plots, …
Show more, hide less
…raincloud plots
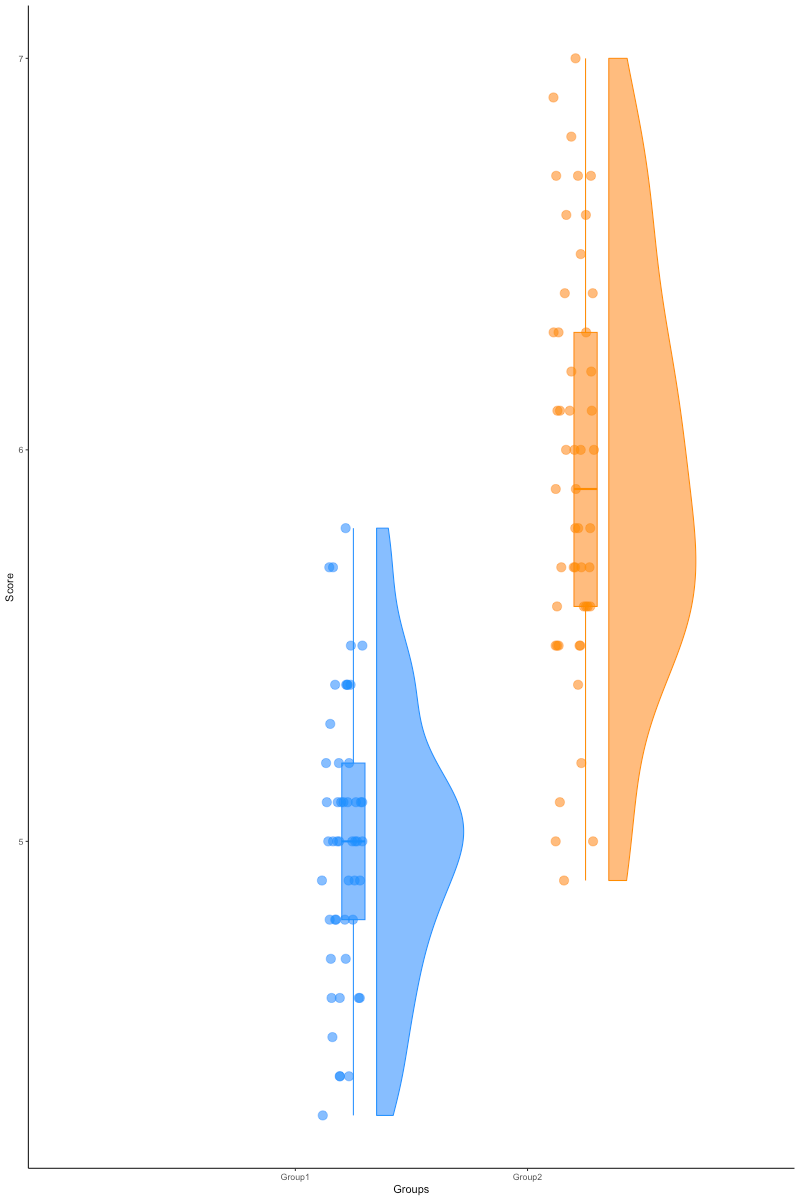
See https://github.com/jorvlan/raincloudplots
Even with repeated measures
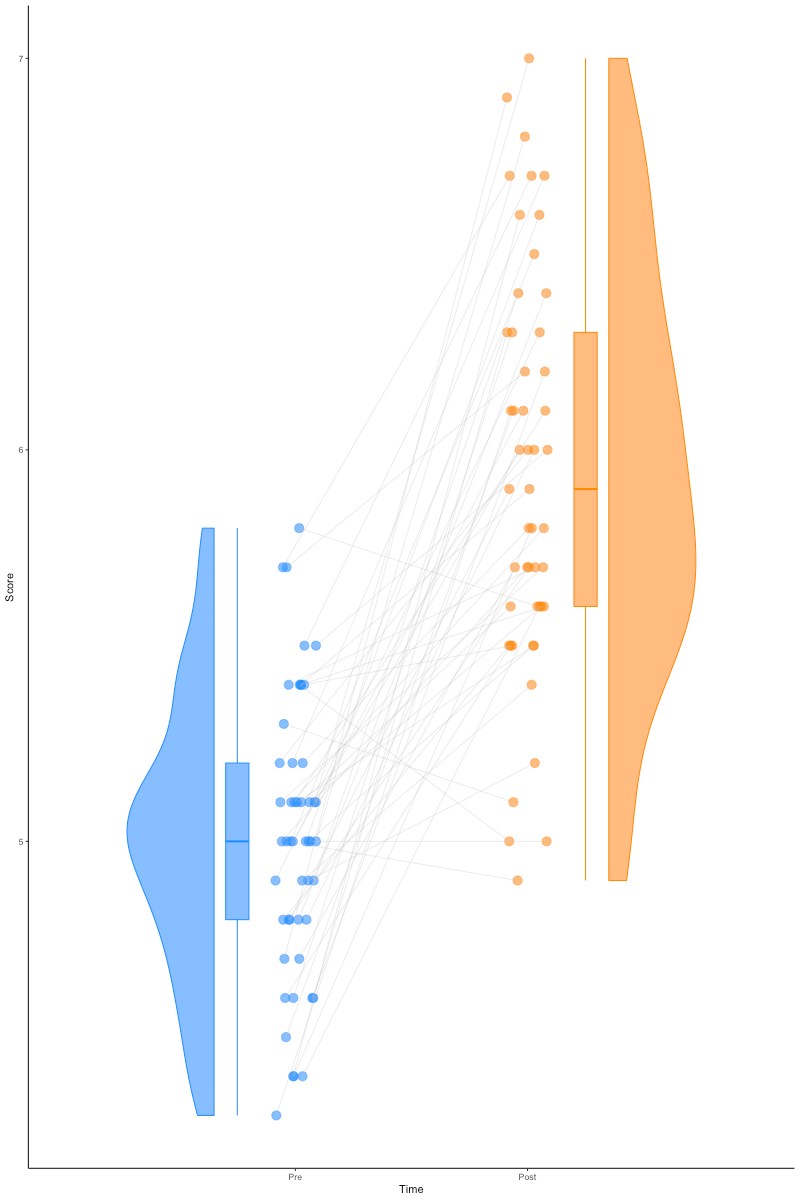
See https://github.com/jorvlan/raincloudplots
Increasing the information density
Using color
- Think about accessibility
- About 5-8% of males + 0.5-1% of females cannot distinguish certain shades of red and green
- Color is itself multidimensional
- Can use hue and saturation/transparency independently
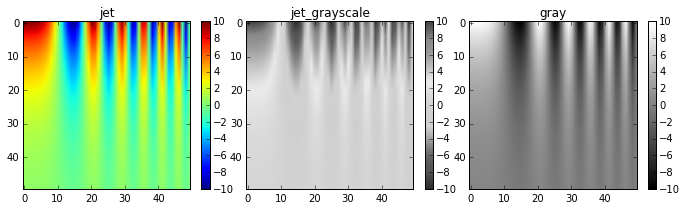
- Using the right colormap matters
- Color maps: each number maps to a color
- Avoid colormaps that are not perceptually uniform
Perceptually uniform colormaps
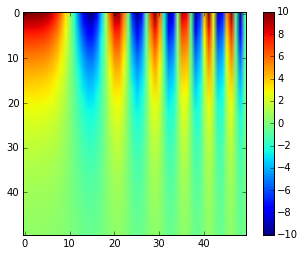
Perceptually uniform colormaps
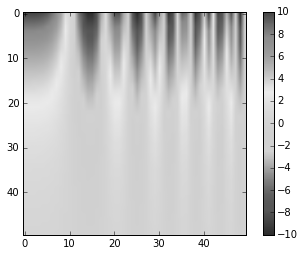
Perceptually uniform colormaps
Solutions?
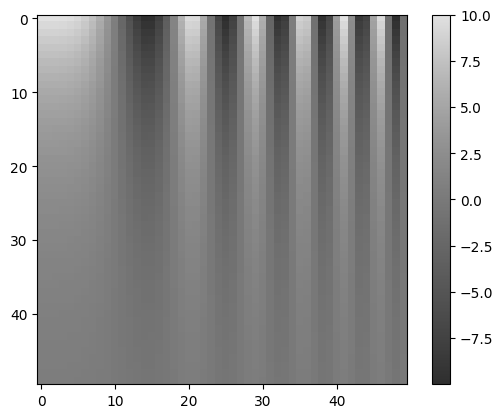
- Use grayscale
- Use a colormap that is optimized for perceptual uniformity
- Viridis
Viridis
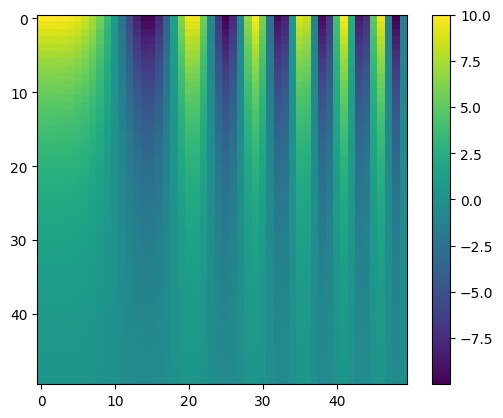
Viridis
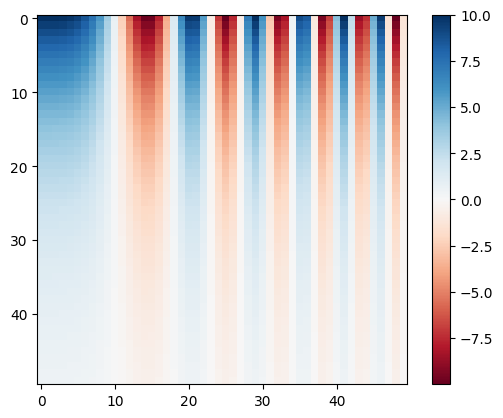
If you need a divergent colormap
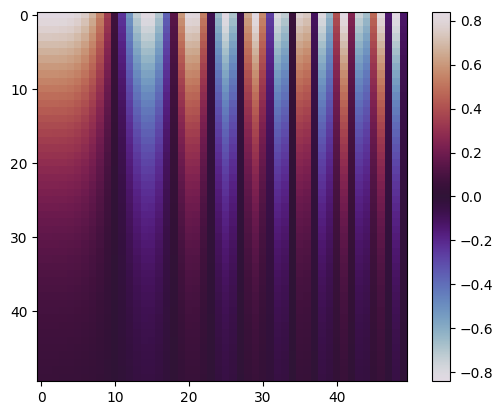
Or a circular colormap
Aligning graphics and concepts
Based on Goldstone et al. (2015)
- Continuous dimensions with continuously perceived graphical attributes:
- Saturation
- Size
- Position along an axis
- Categorical dimensions with categorically perceived graphical attributes:
- Hue
- Shape
- If using time (e.g., in animation) match that with time in the experiment.
- If that’s a relevant dimension.
So, have we solved the curse of dimensionality?
Using animations
Can help with visualization of complex three-dimensional structures

Or events unfolding over time (we’ll see an example below)
Using interactions
Provides a way to explore the data or link between different attributes
Using interactions
Dimensionality reduction approaches
“To deal with hyper-planes in a 14-dimensional space, visualize a 3D space and say ‘fourteen’ very loudly. Everyone does it.” - Geoff Hinton
- Linear dimensionality reduction: PCA
- Non-linear approaches:
- t-SNE
- UMAP
- …
Demo
Where does t-sne (and similar) shine?

Where does t-sne (and similar) shine?
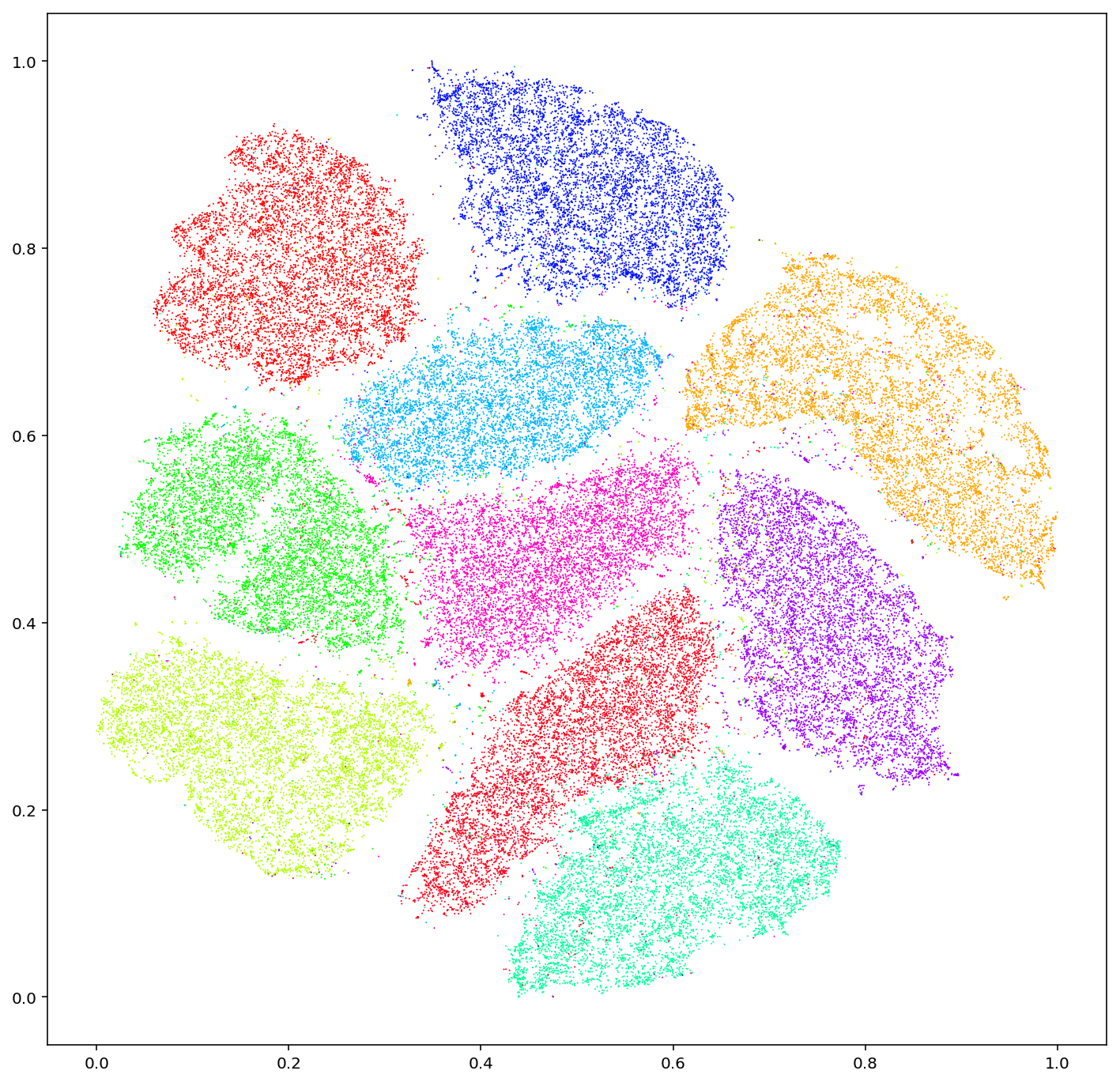
Where does t-sne (and similar) shine?
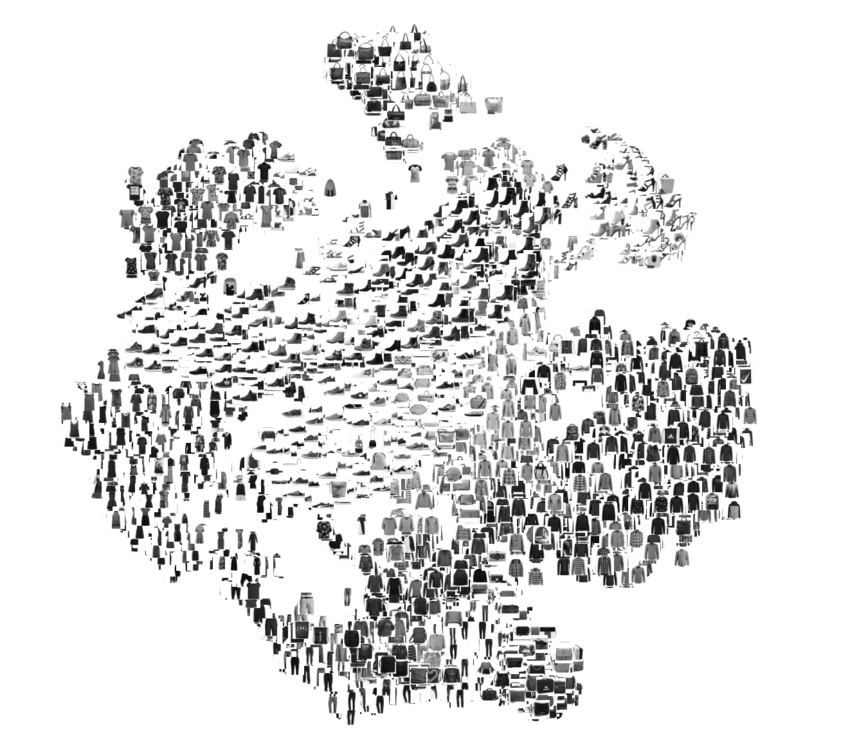
Combining dimensionality reduction and animation

https://hypertools.readthedocs.io/en/latest/