Machine learning

What is machine learning (ML)

• A field of science/engineering that builds systems that are capable of learning from experience.
• Very broad and varied, but some common features:
  • Algorithms that learn from data, rather than rule-based, hand-tuned systems.
  • Performance evaluation focused on well-defined quantitative targets.
• A contrast with “traditional inference”:
  • Focused on “prediction”.
  • Not as much on “explanation” or “understanding”.

The setup

• Let \(X\) be a set of independent variables, \(n\) rows by \(p\) columns.
• Let’s assume it’s tidy 😊
• \(y\) a dependent variable, \(n\) entries
• So, in fairly general terms:
• \(y = f_\theta(X)\)
• Where \(f\) is some function and \(\theta\) are parameters of this function.
• The goal of ML can be described as defining a procedure that identifies the values of \(\theta\)
• In some cases, also need to learn the form of \(f\)

Types of ML

• Supervised:
  • In this case, we have both \(y\) and \(X\) measured.
  • Predicting people’s chronological age from structural brain differences.
  • Determining whether an email is spam.
  • Predicting a person’s rating of a movie based on their rating of other movies.
• Unsupervised:
  • In this case, we only have \(X\) (\(y\) may be a latent factor).
  • Example from Efron and Diaconis: determining the linear combination of grades that best distinguishes between students.
  • Determining sub-types of autism based on brain structure

Supervised learning

• Regression: \(y\) is a continuous variable
• Classification: \(y\) is a discrete variable

Regression

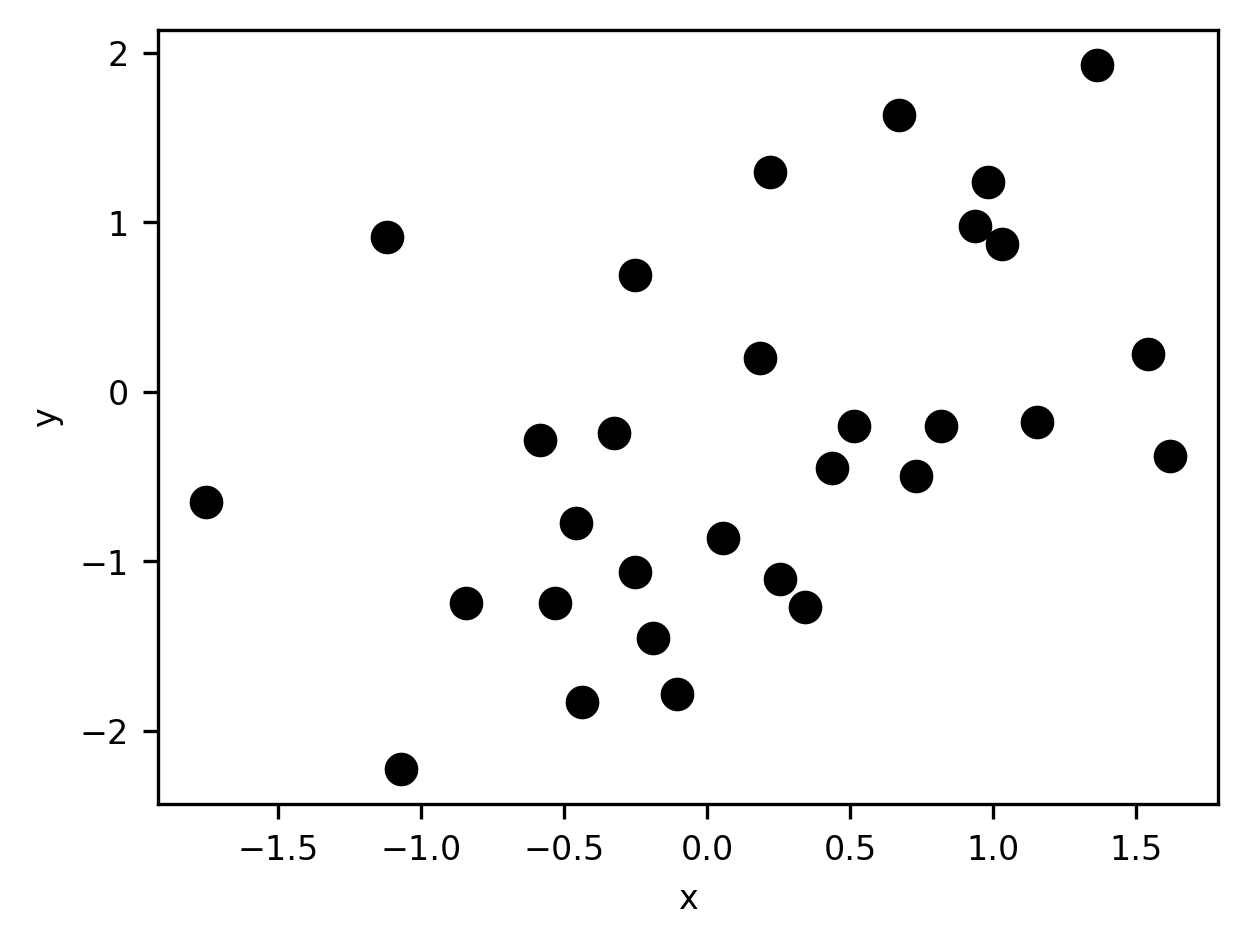
Regression

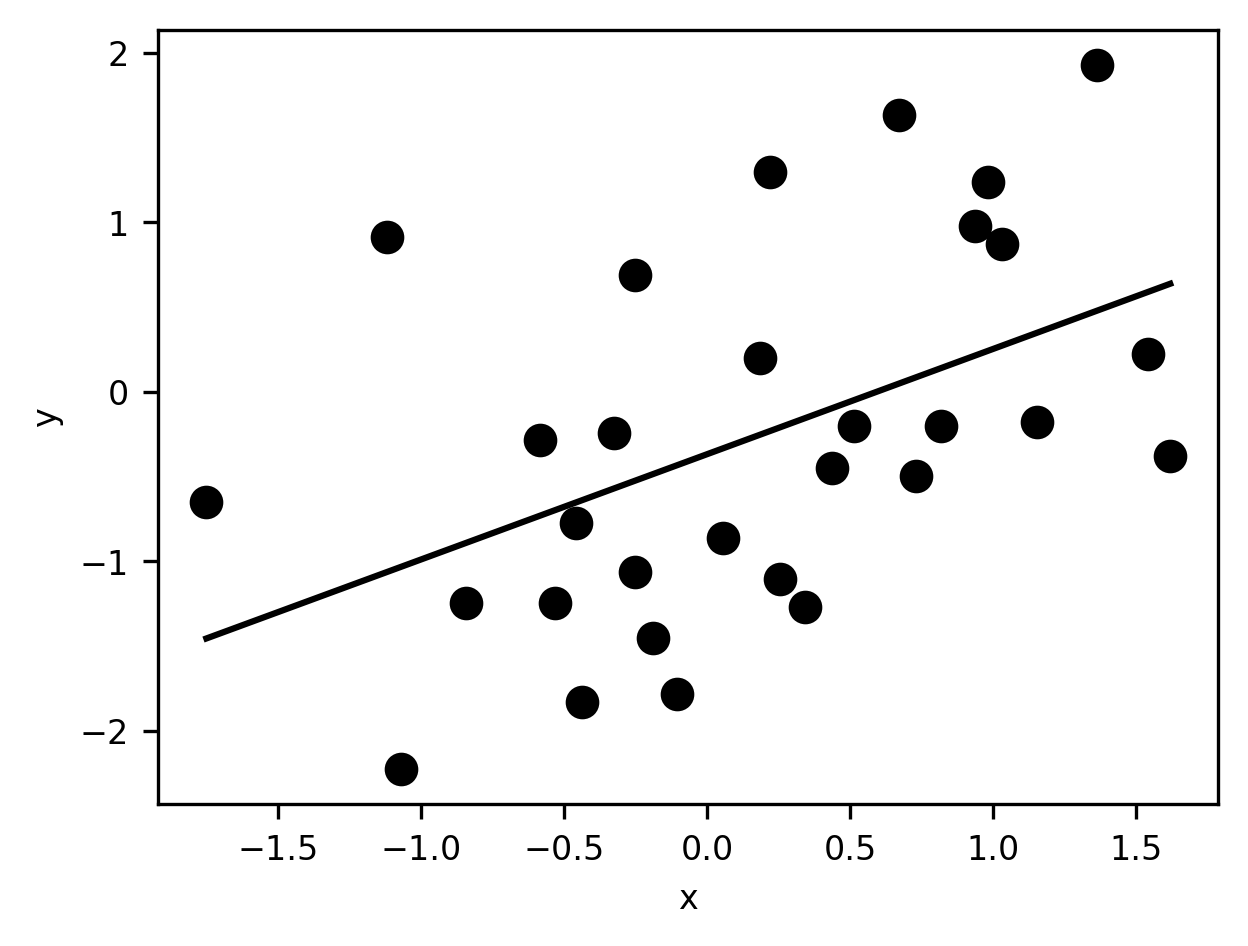
Classification

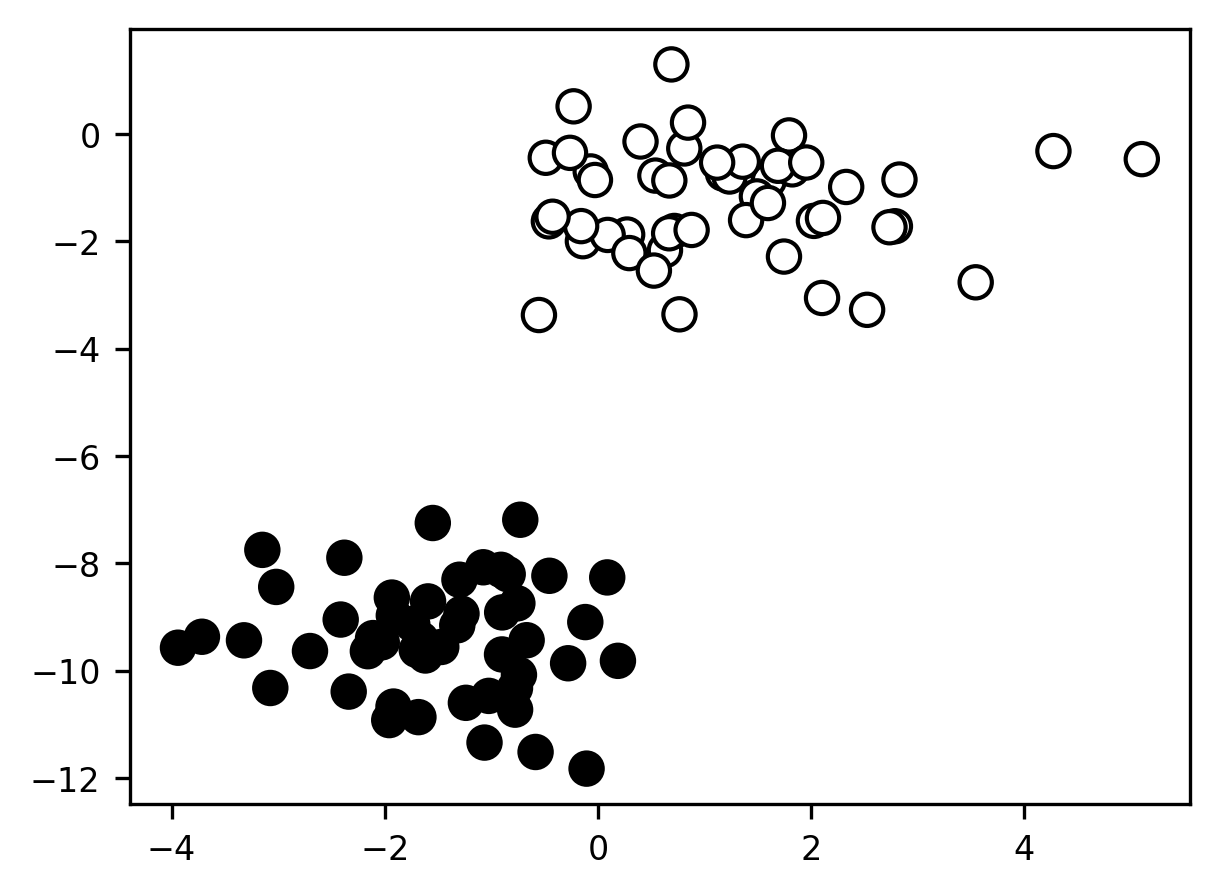
Unsupervised learning

• Clustering
• Dimensionality reduction

Clustering

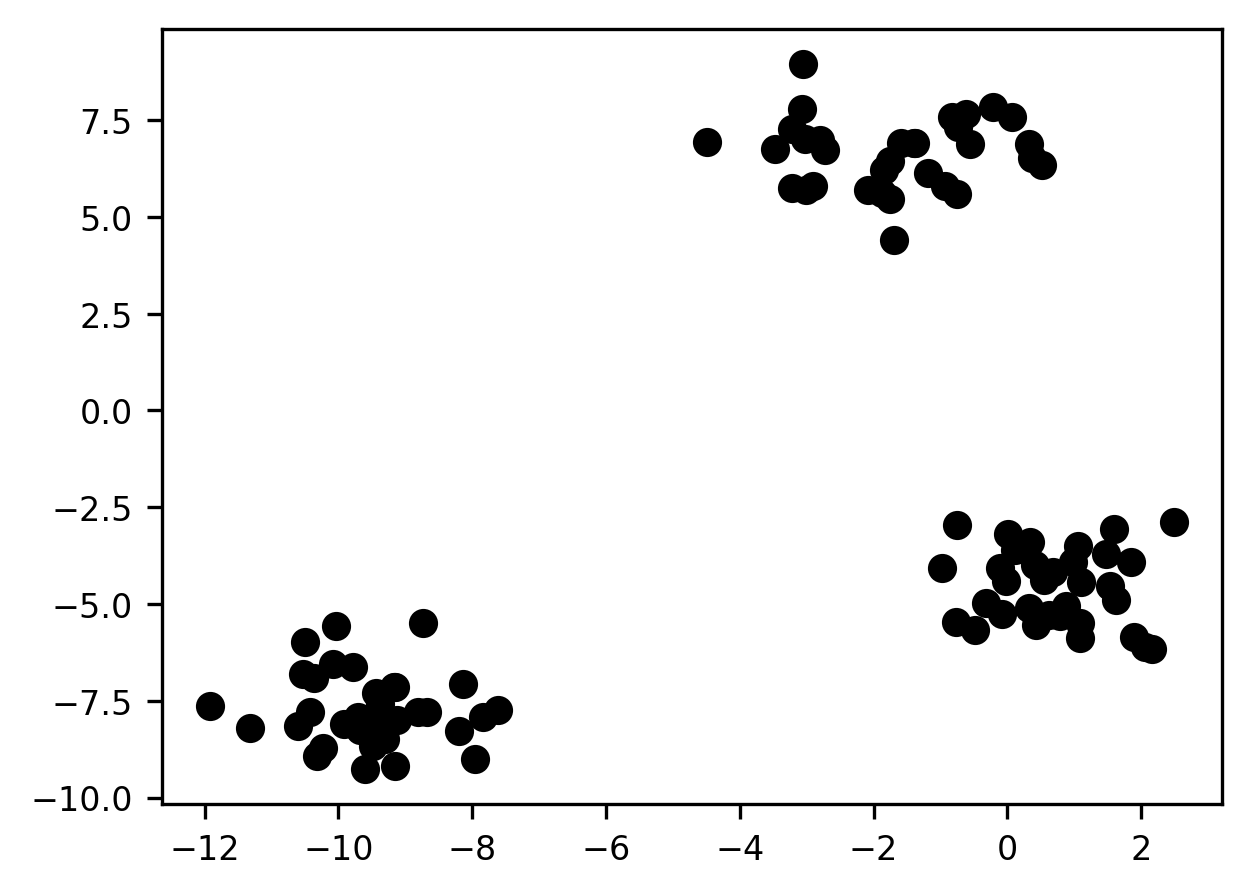
Clustering

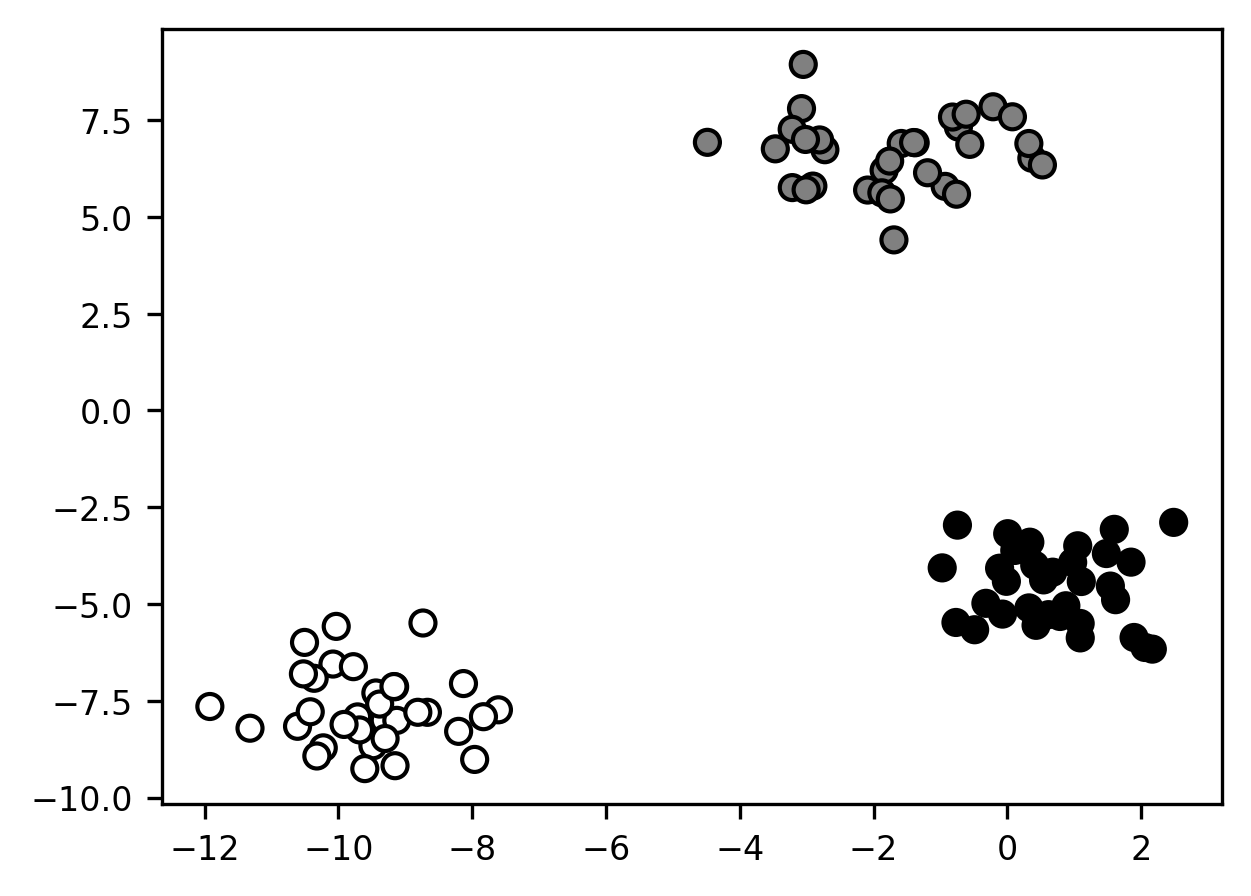
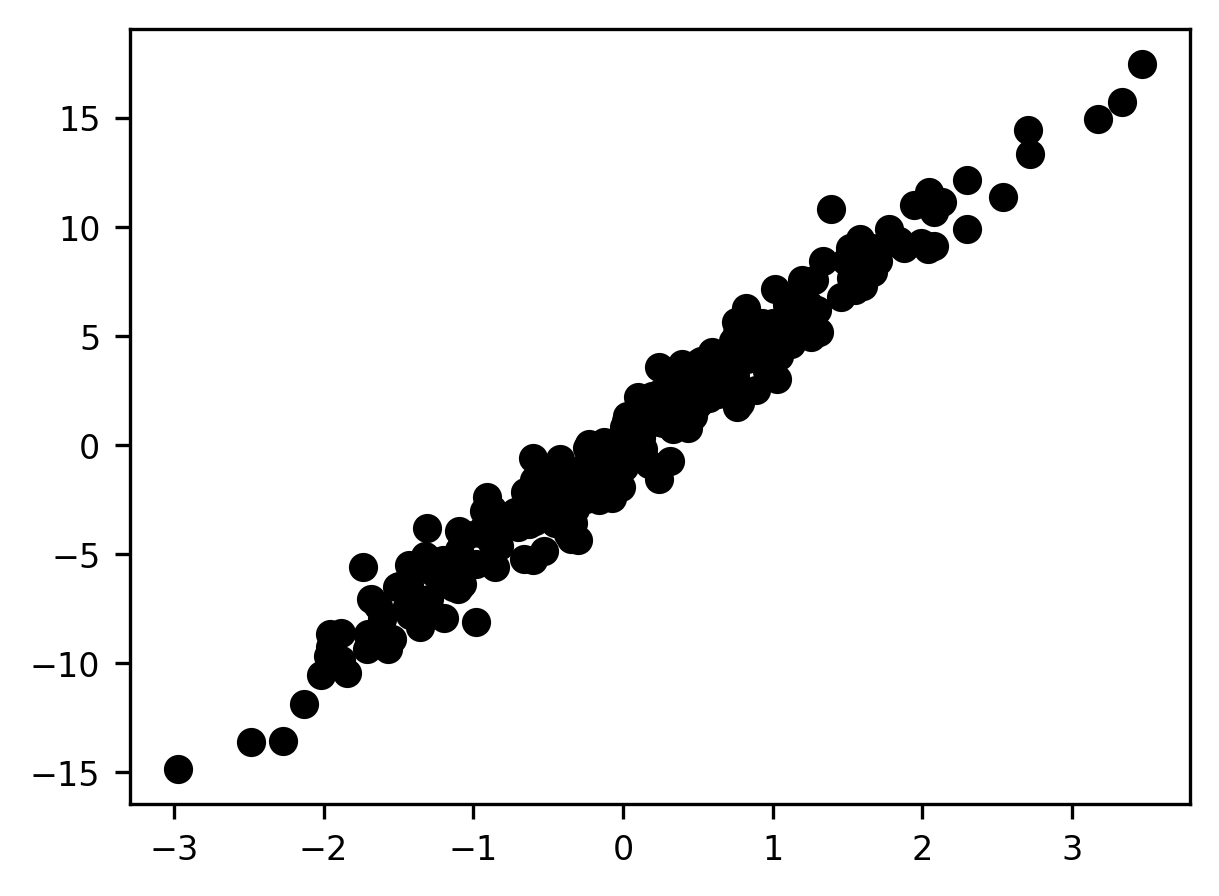
Dimensionality reduction

Quantifying performance

Quantifying performance

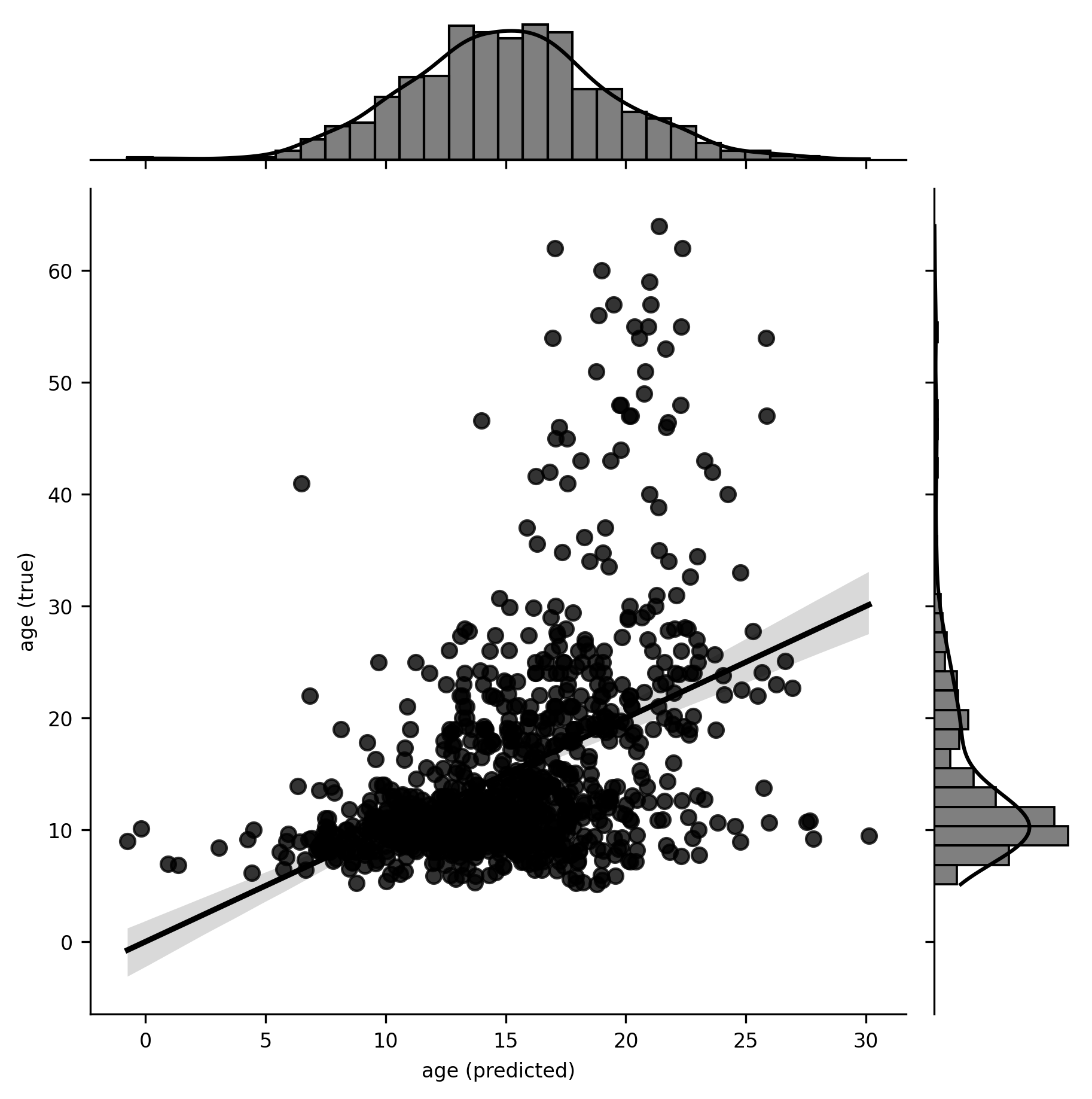
\(R^2 = 1 - \frac{SS_{res}}{SS_{tot}} = 1 - \frac{\sum{(y - \hat{y})^2}}{\sum{(y - \bar{y})^2}}\)

\(R^2 = 0.2\)

Quantifying performance

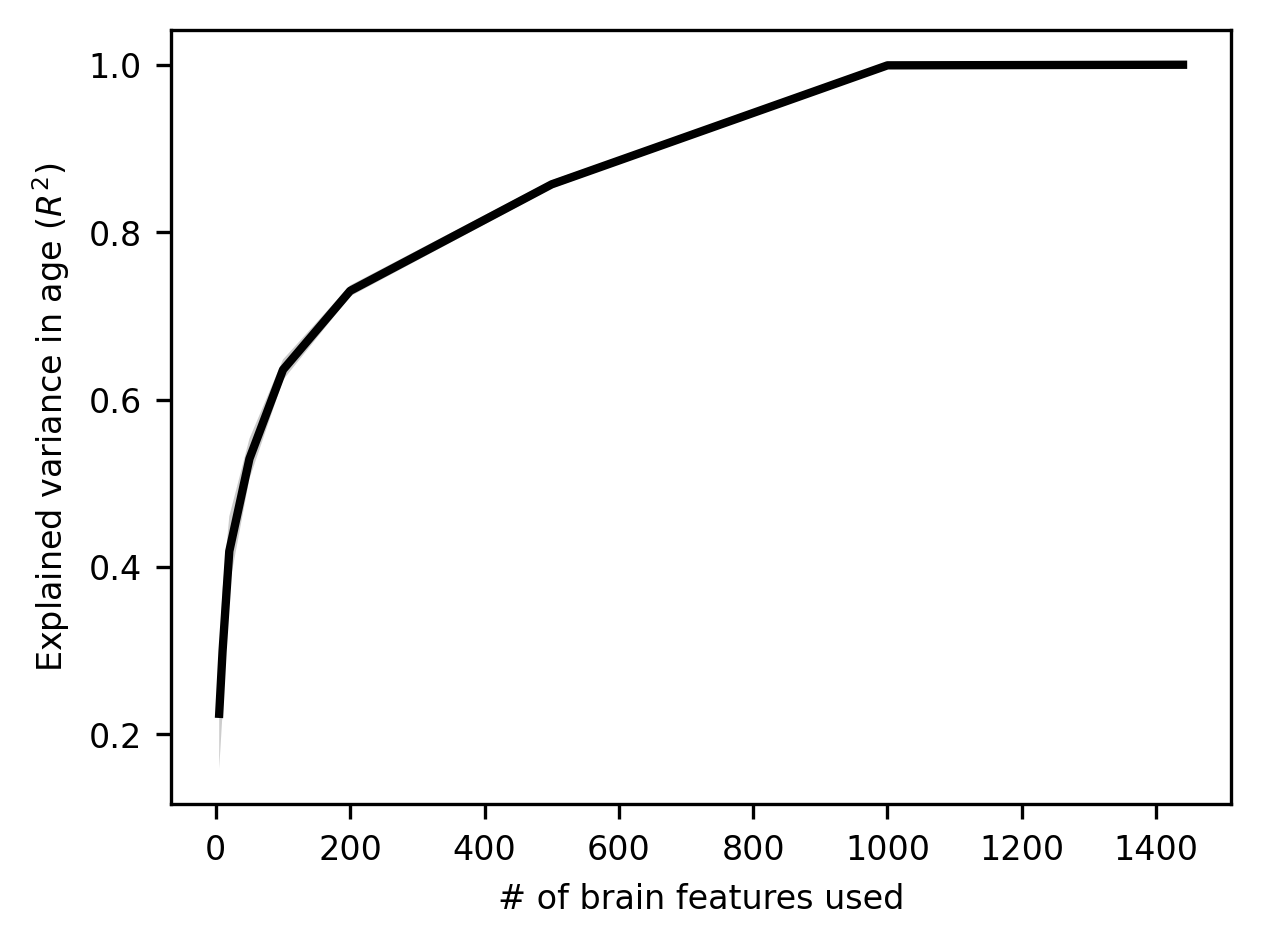
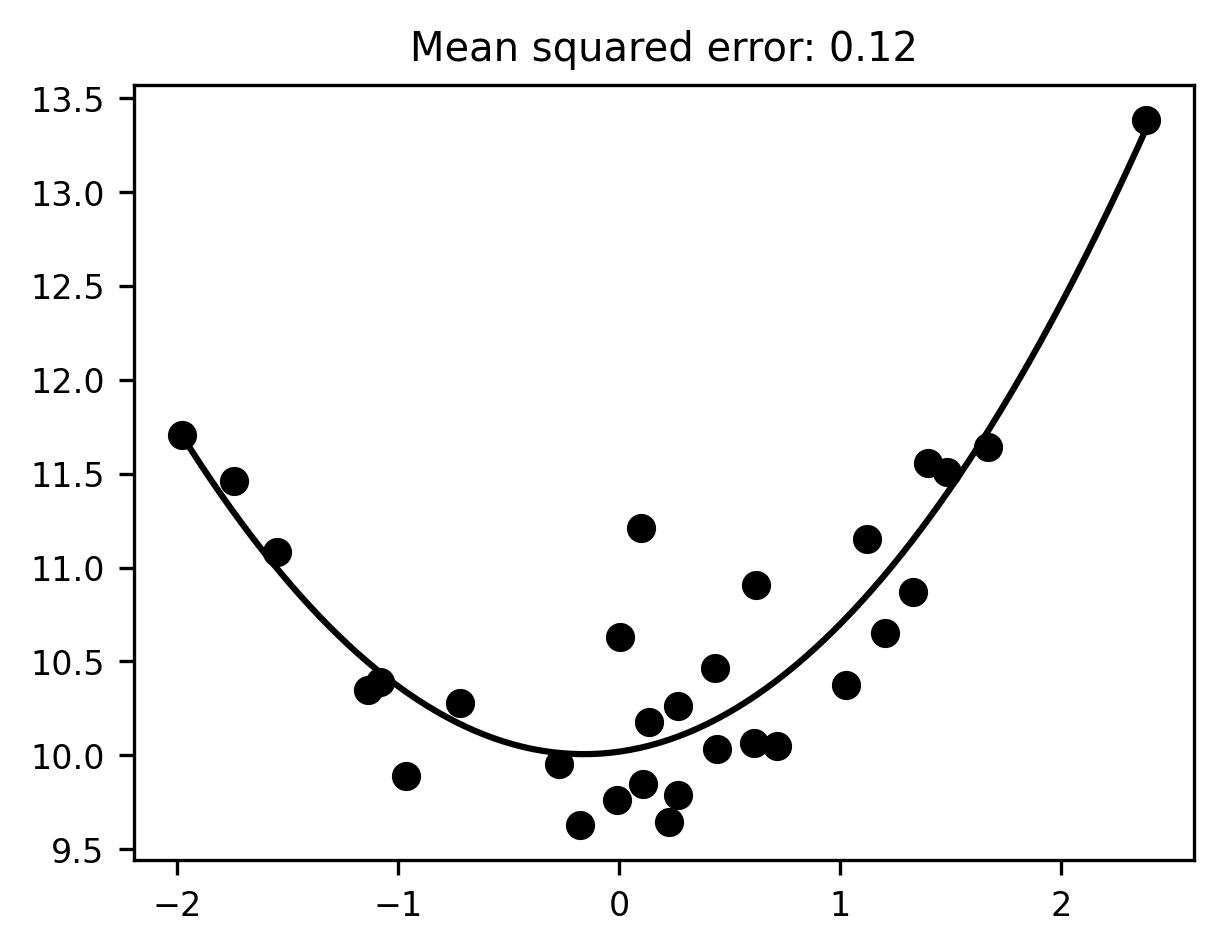
Overfitting

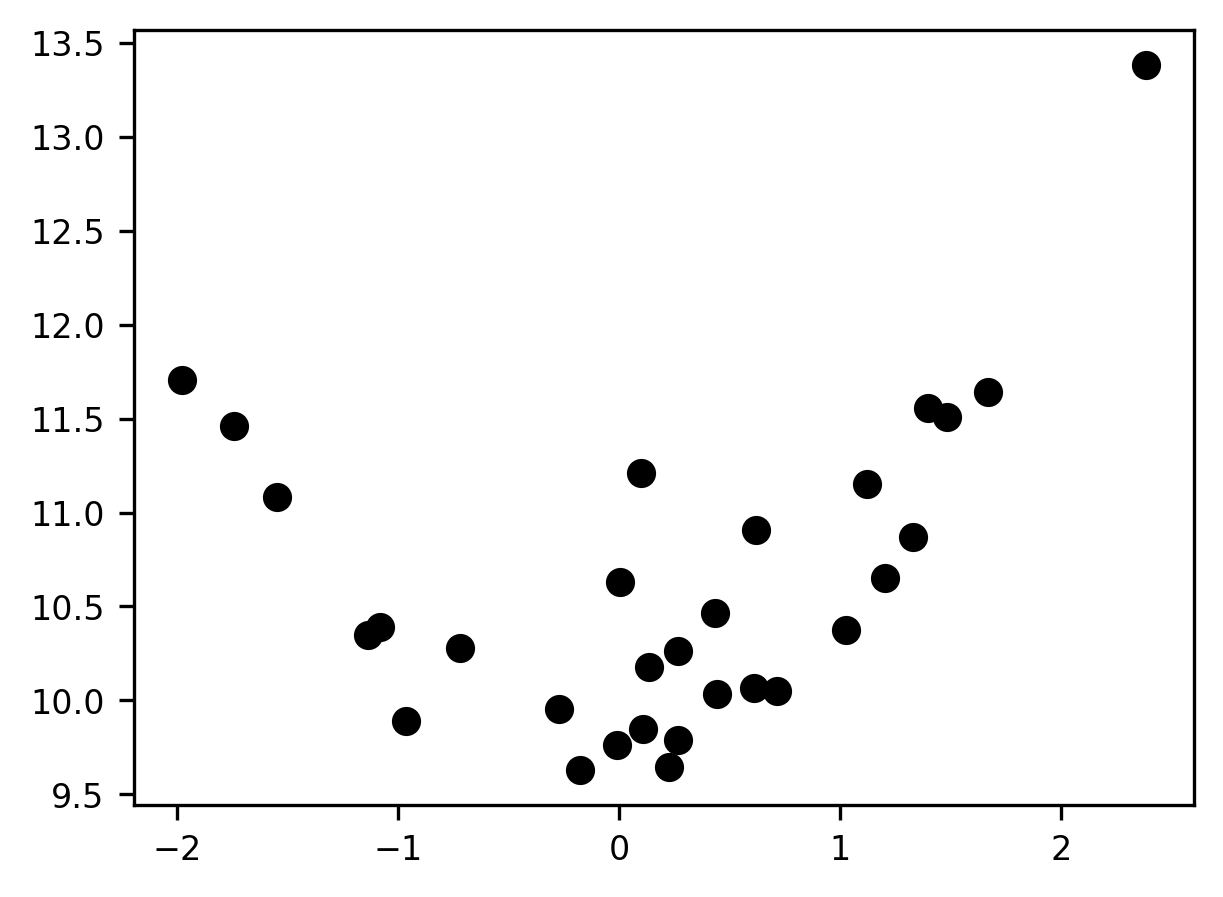
Overfitting

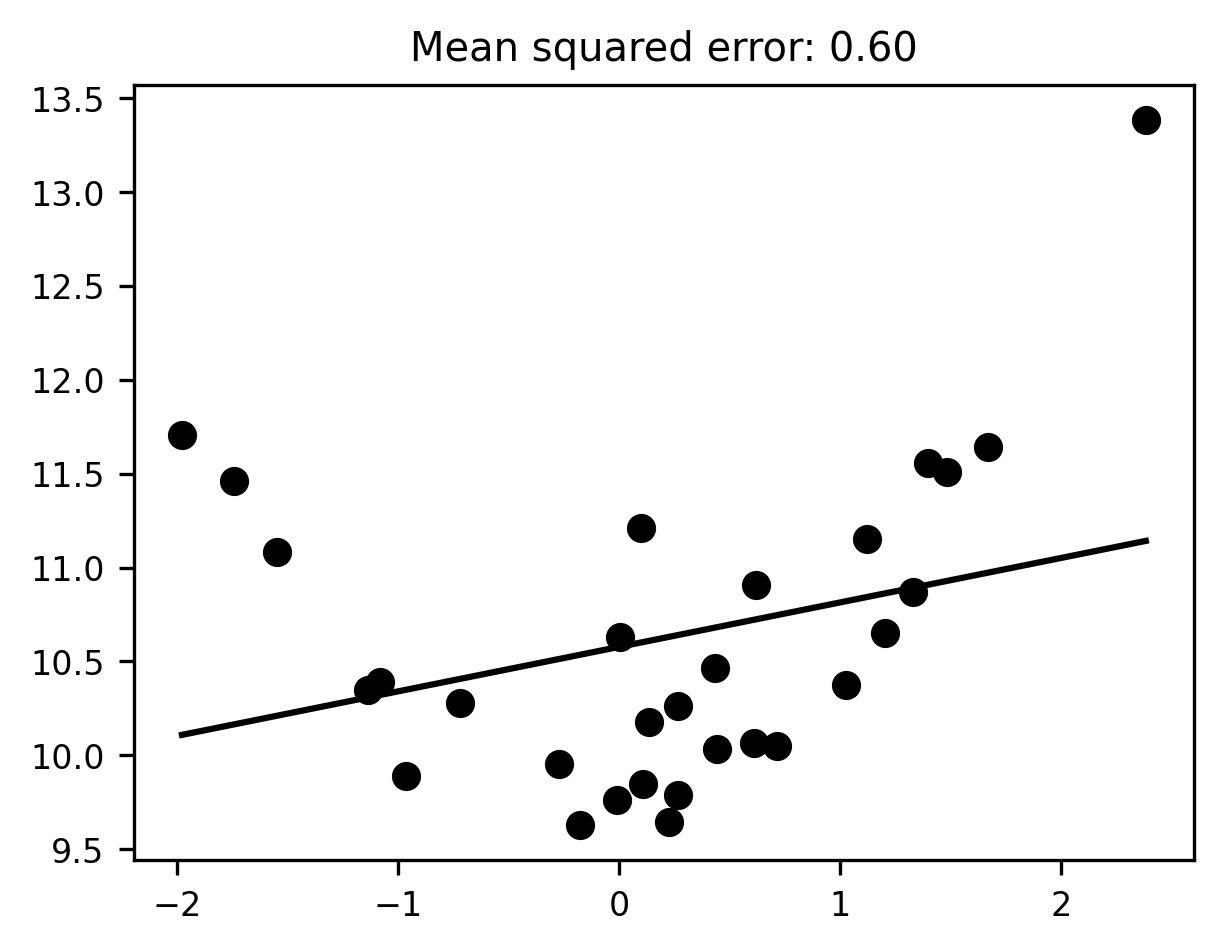
Overfitting

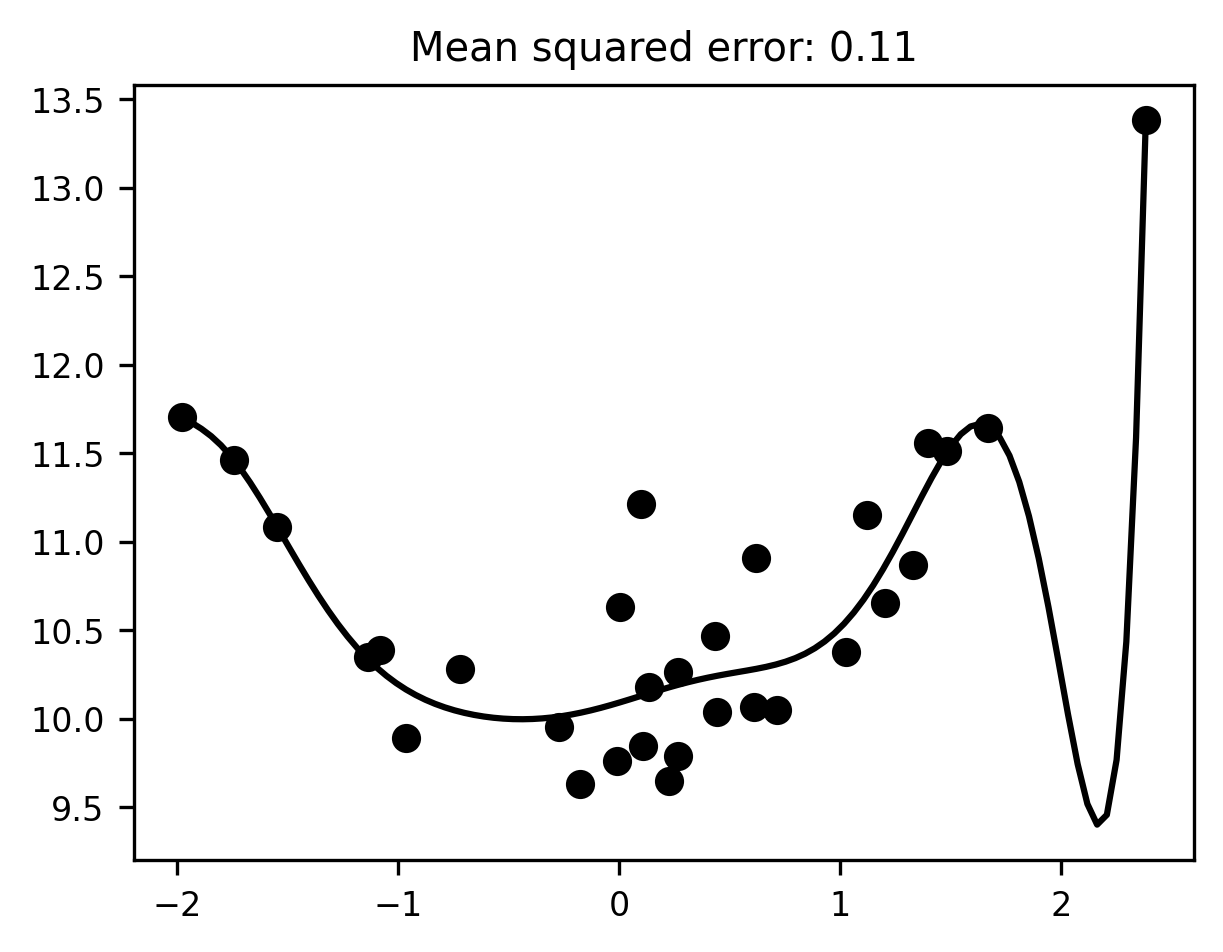
Overfitting

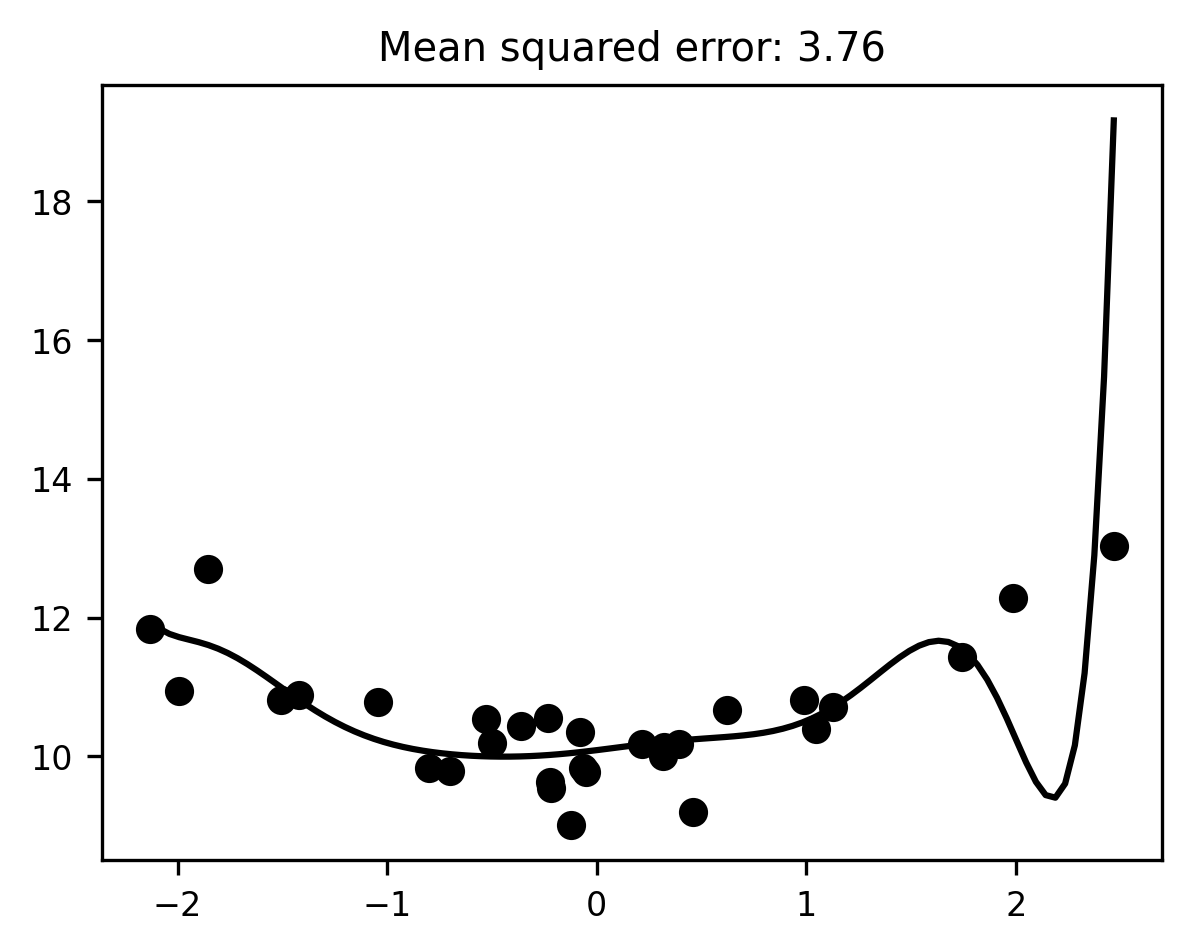
Overfitting

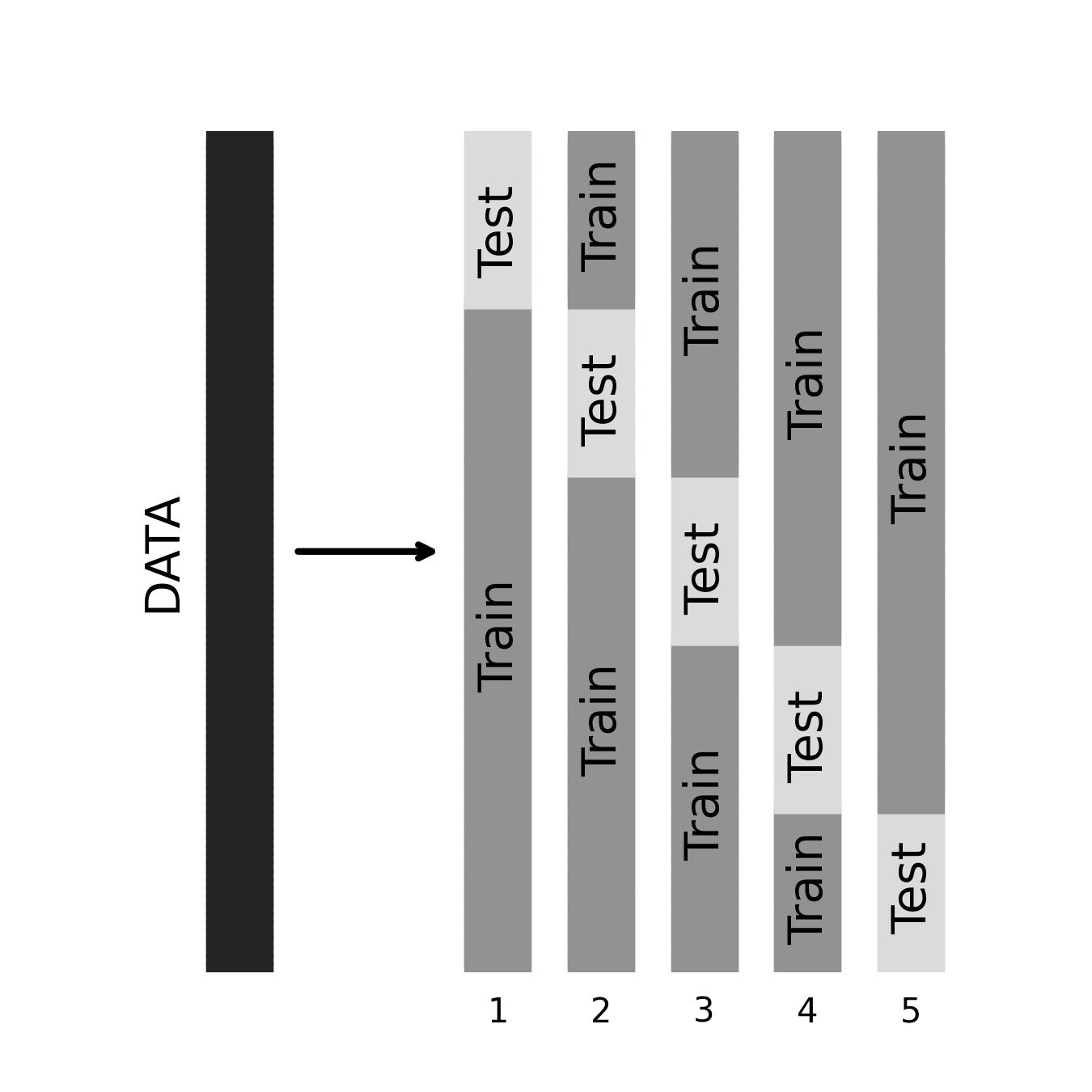
Cross-validation

Model selection

• Consider: \(y = X\beta\)
  • Fitting: solve for \(\beta\)
  • OLS: minimize \(\sum{(y - \hat{y})^2}\)
  • But what about the setting where \(p\) >> \(n\)?
  • Or with correlated regressors?
  • The curse of dimensionality
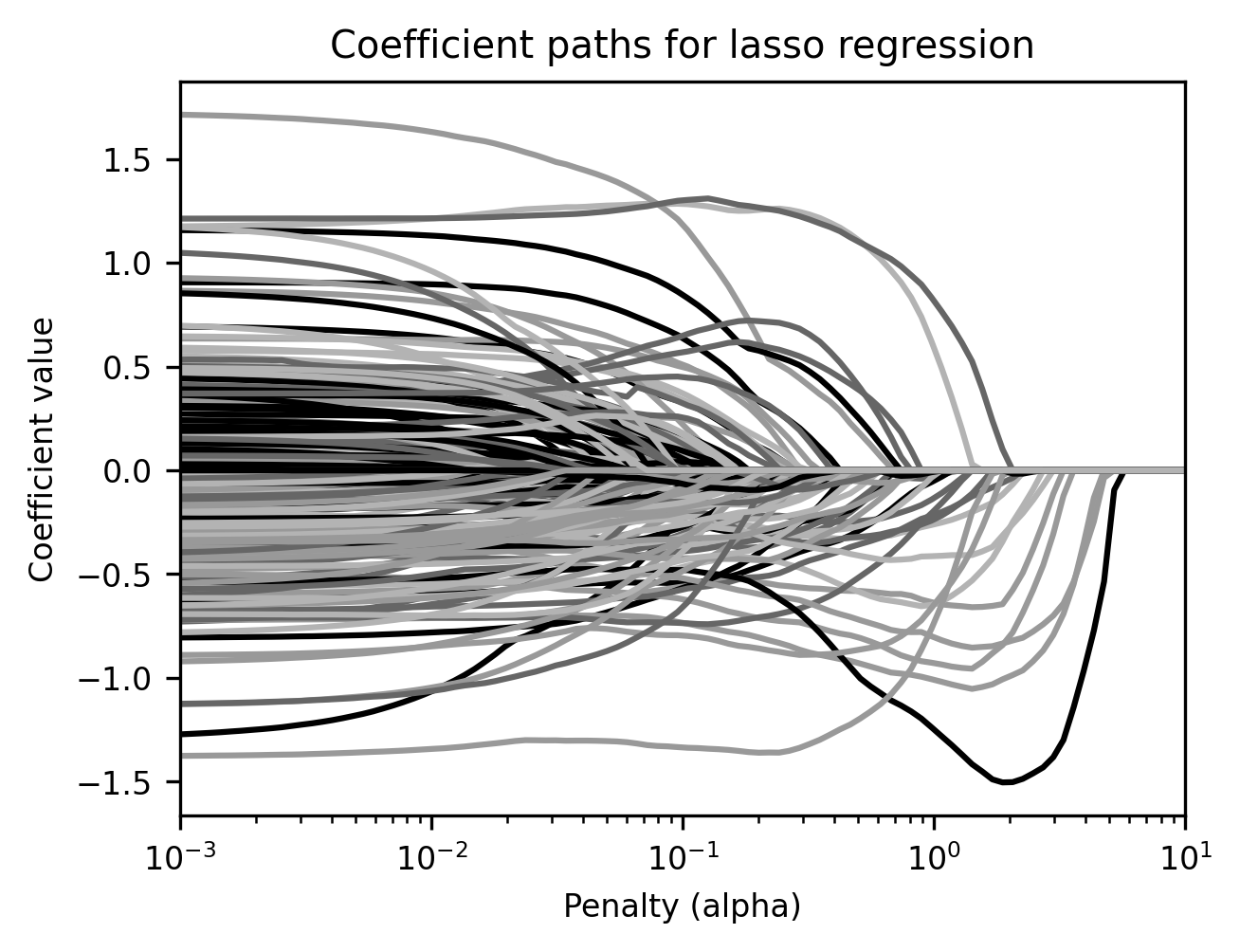
• Lasso: solve for beta
  • Minimize: \(\sum{(y - \hat{y})^2} + \lambda \sum{|\beta|}\)
  • Where \(\lambda\) is a hyperparameter

The bias variance tradeoff

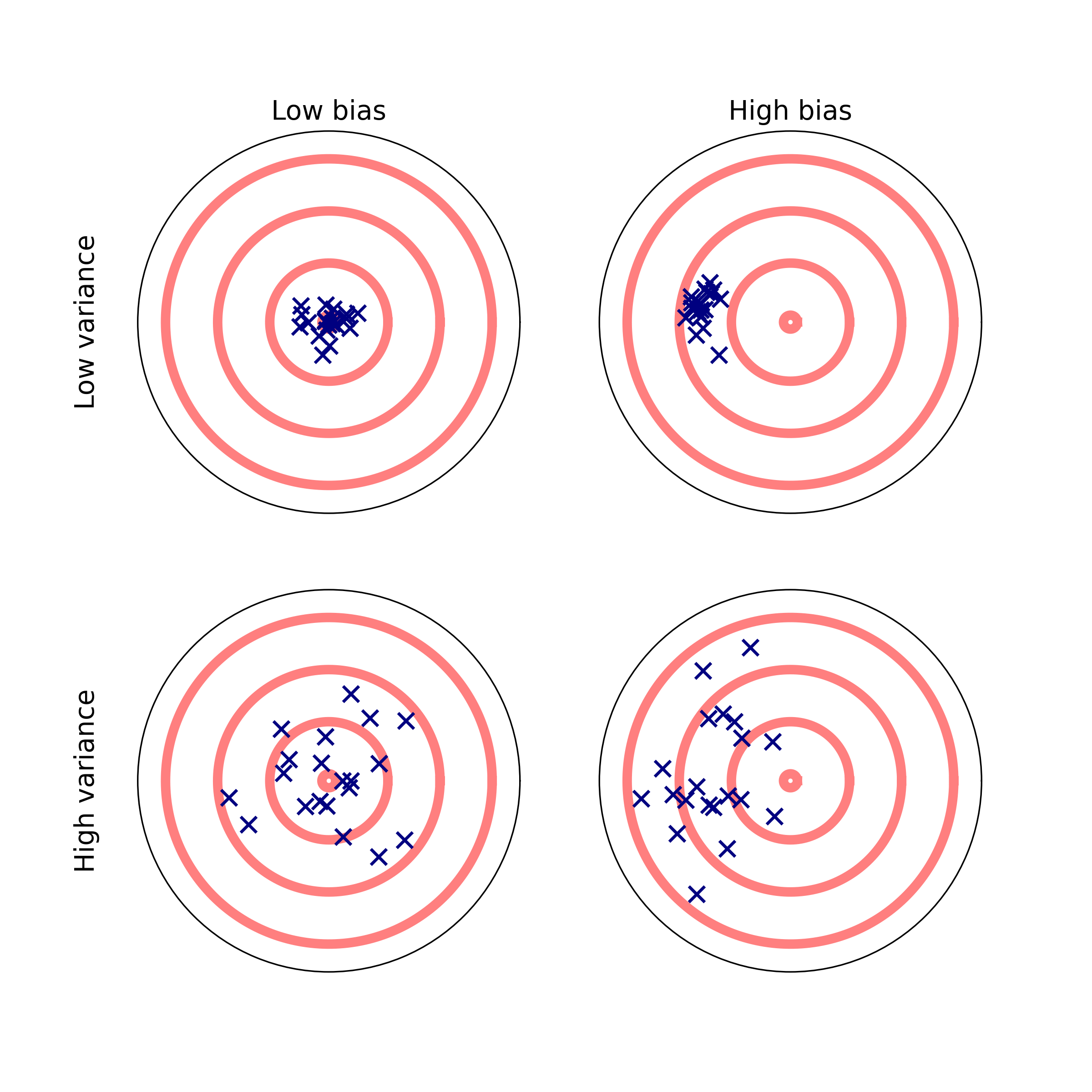
But how do we know how much bias?

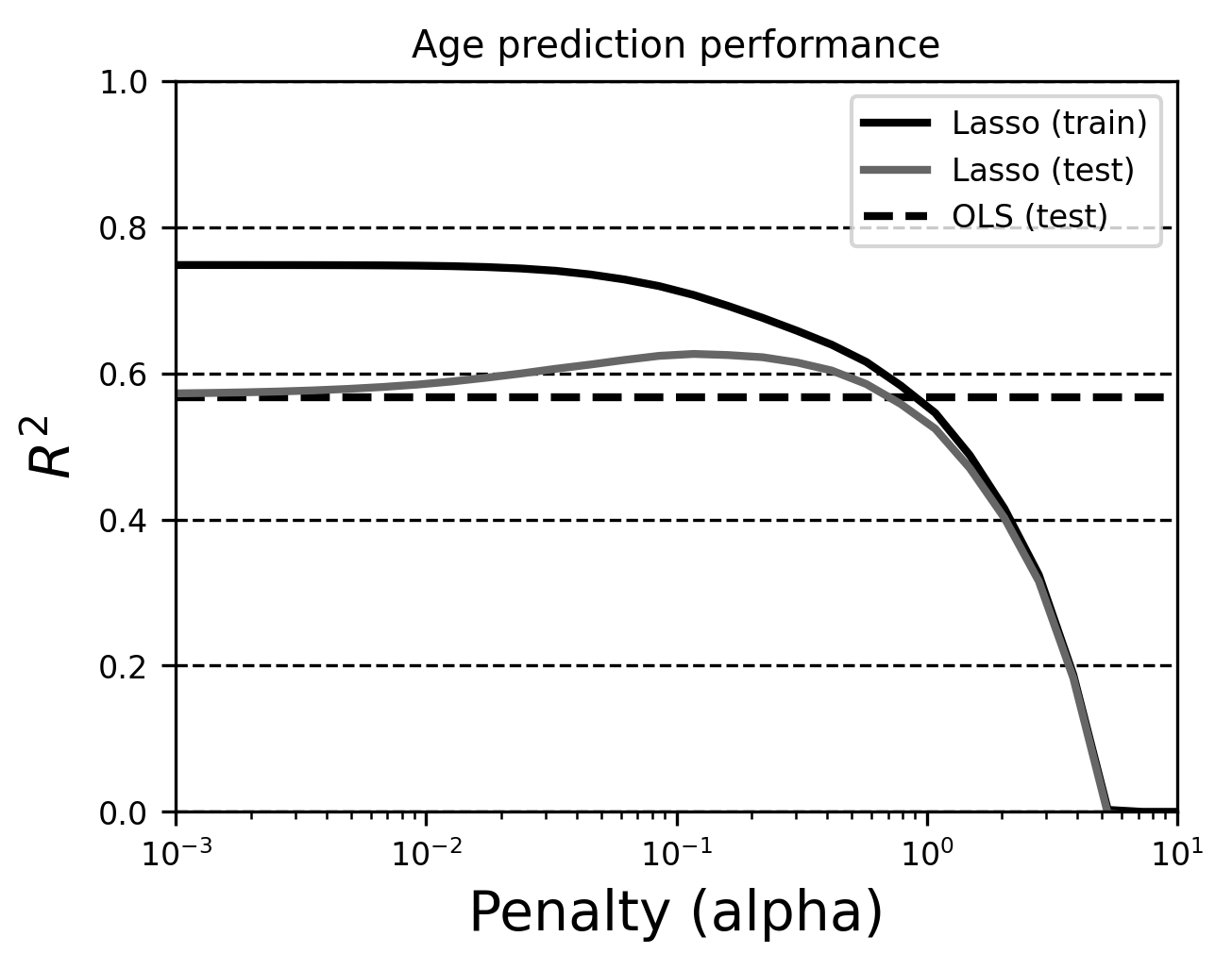
Lasso

Cross-validation for model selection

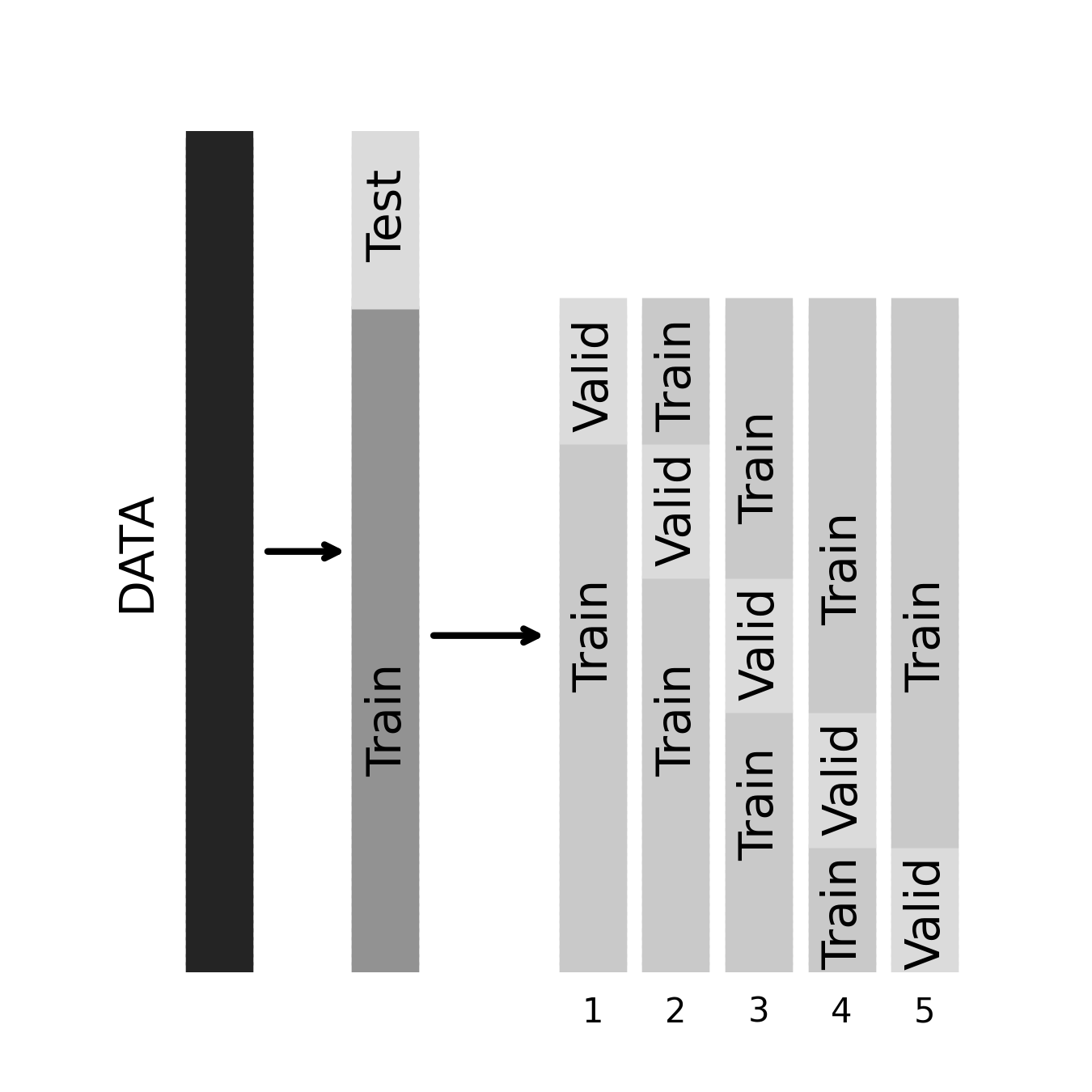
Cross-validation for model selection